非平衡・非定常の世界を解明する――統計物理学における新たな挑戦 ―先端物理学科 秋元琢磨教授に聞く― 

     

統計物理学とは、分子などの粒子がたくさん集まった時のふるまいを、確率や統計の概念を使って考える学問です。今では物理現象の範疇を超えて広くいろいろな対象に適用されるようになったこの学問分野には、しかし未解決な問題が残っています。秋元琢磨教授は、「無限測度エルゴード理論」という数学の理論を利用して、その問題の一つの解明に挑んでいます。統計物理学とは何か。その研究からどんなことが見えてくるのか。「研究教育」への熱い思いとともに、秋元教授が語ります。

秋元 琢磨（あきもと たくま） 2001年 早稲田大学理工学部応用物理学科卒業、2007 年 同大学 理工学研究科物理学及応用物理学 博士課程修了。博士（理学）。慶應義塾大学理工学研究科講師、同准教授などを経て、2017年より東京理科大学理工学部物理学科 准教授。2025年より現職。

「多数の粒子のふるまい」を解き明かす統計物理学

――秋元先生の研究の概要を教えてください。

私が専門としているのは統計物理学です。ひとことで言えば、分子などの粒子がたくさん集まった時のふるまいについて考える学問です。膨大な数の粒子一つひとつを追うことはできないのでその全体のふるまいを確率や統計に基づいて考える、ということが基本になります。最も代表的な例は、気体分子の運動を統計的に扱うことで気体の状態（温度や圧力、エネルギー）を計算する気体分子運動論で、元々はそのような物理学の世界を理解するための学問として発展しました。しかしいまでは、例えばここでいう気体分子を人間に置き換えることで、株価など、多数の人間の行動によって変化する経済の動きを考えるなど、統計物理学は広くいろんな対象に応用されるようになっています。

そうした中で、私は、統計物理学に残る基礎的な問題について研究をしています。具体的には、非平衡・非定常の系の現象を説明する基礎理論を「無限測度エルゴード理論」を用いて構築しようという研究です。……と急に言っても、何のことかなかなかわかりづらいと思いますので、順を追って説明していきますね。

――「非平衡・非定常の系」のあたりから一気に難しそうになりました……。

そうだと思います。ではまず、前提として「平衡」と「定常」から説明すると、平衡とは、ひとまとまりの気体など（＝系）において、気体の流れがなく、圧力や温度が変わらず一定の状態を保っていることです。また、定常とは、流れがあっても時間的に変化せず一定の状態を保っていることです。簡単な例で言うと、外から熱を加えられたりしていない密閉された容器中の理想気体は平衡の状態にあります。一方、トンネルのような容器の中を、気体が一定の速度と密度で、入口から出口に向かって流れ続け、時間が経っても変化しないのが定常の状態です。

平衡の統計物理学はほぼ完成していると言われている一方、非平衡については未解決な問題が多く残っています。中でも、非平衡でかつ非定常の状態というのは特に扱うのが困難です。その非平衡・非定常状態に、無限測度エルゴード理論というものでアプローチすることで、未解決の問題を解明しようというのが、私が取り組んでいる研究になります。

非平衡・非定常の世界に挑む

――では、無限測度エルゴード理論とはどのようなものなのですか。

まず「エルゴード理論」とは何かと言えば、これは、時間平均と空間平均の関係を扱う数学の理論です。サイコロを例に考えてみましょう。時間平均というのは、複数回振った時の平均の値です。１～６の目が出る確率が等しいとすれば、無限回振ると、最終的には1～6の目の平均である3.5に近づいていきますが、それが時間平均です。一方、空間平均というのは、目の分布だけから得た平均で、これは（1+2+3+4+5+6）/6＝3.5となります。そしてこの例のように、「時間平均＝空間平均」の関係が成り立つ性質のことを「エルゴード性」と言います。気体分子を例に考えると、箱の中に気体分子を閉じ込めると気体分子は箱全体に広がっていき、最終的には分子は箱の中の空間に均一に広がると考えられます。つまり、時間平均＝空間平均となっているので、これもエルゴード性の例と言えます。

続いて「無限測度」ですが、まず測度とは、ここでは確率と同じと考えて差し支えありません。そして無限測度のイメージをサイコロに例えて考えると、目が無限個あるサイコロを投げた場合に相当します。目が１～６までの普通のサイコロは、一つの目が出る確率は1/6で、いずれかの目が出る確率の合計は１になります（＝全ての目の確率を足すと１になるように「規格化できる」）。これが有限測度です。一方、目が無限個あるサイコロの場合、一つの目が出る確率は1/無限大、つまりゼロになってしまいます。そのため、いずれかの目が出る確率の合計が１にならない（＝規格化できない）。これが無限測度のイメージです。そして、無限測度の状態においては「時間平均＝空間平均」は成り立たない、つまり、エルゴード性が破れる、というのが無限測度エルゴード理論なのです。

無限測度という概念は、非平衡・非定常状態において現れるのではないか——。
そんな思いを抱いたのは、大学院生の頃でした。以来、その考えを確かめようと、無限測度エルゴード理論を用いて非平衡・非定常現象の解明に挑んできました。

――なるほど……。非平衡・非定常状態を、無限測度エルゴード理論によって説明するということのイメージが、なんとなく見えてきました。ただ、実際の物理現象とはどのようにつながるのでしょうか。

無限測度エルゴード理論自体は数学の話なので、まさにそれが実際の物理現象とどう関係してくるかが統計物理学の研究としては重要ですが、最近、その具体的な例を示すことができました。分子にレーザー光を当てることで温度を下げるレーザー冷却という冷却法があるのですが、その一つに「サブリコイル冷却」があります。これは、従来のレーザー冷却では原理的にこの温度をより低温にはできないとされていた限界の温度を越えてさらに低い極低温まで冷やすことができるという技術なのですが、このサブリコイル冷却の系がまさに非平衡・非定常の状態にあります。この冷却の際に起きている現象のメカニズムは解明されていないのですが、私はここに無限測度が表れるということを最近、示すことができました。

――つまり、現状では、サブリコイル冷却がなぜ起きるのかははっきりと解明されていないものの、無限測度エルゴード理論を用いると、そのメカニズムがより厳密に説明できる可能性がある、ということでしょうか。

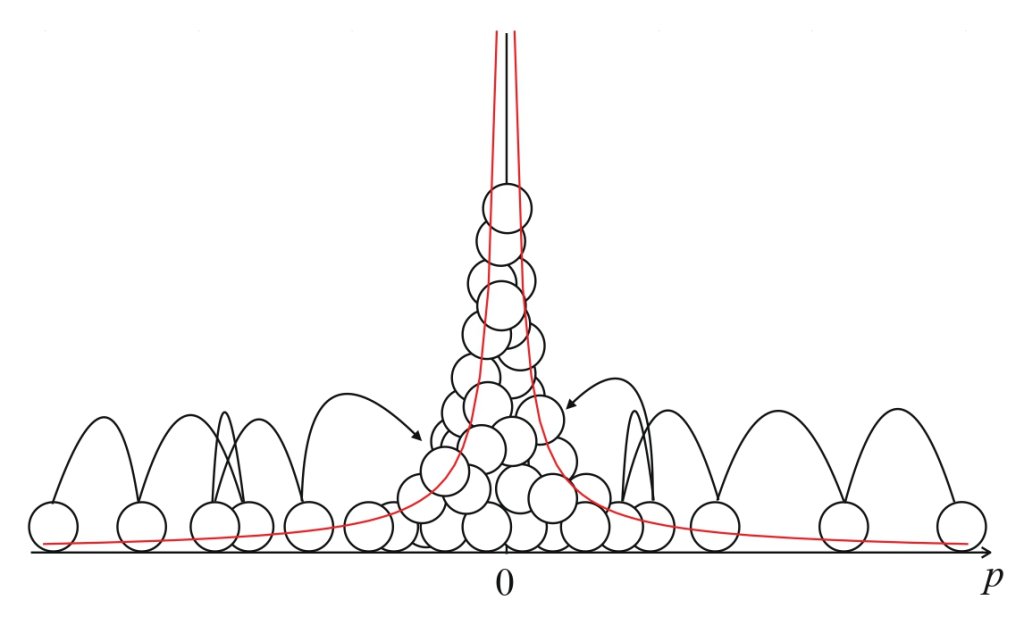
ざっくりと言えばそういうことになります。サブリコイル冷却は、様々な技術への応用も期待されるとても重要な発見で、発見者はノーベル賞を受賞しています。そのような現象の理論面の解明が、無限測度エルゴード理論によって可能になるかもしれないと考えています。目標とする段階に至るまでにはまだいろいろな難題があるのですが、それらを乗り越えるべく、研究を続けています。また一方、この研究では、無限測度エルゴード理論という数学の理論によって物理現象の理解を深めようとしていますが、この研究を進めることで逆に、無限測度エルゴード理論自体も進化して、数学の発展にも寄与できたら、という気持ちもあります。

「拡散現象の研究」や「地震の種類判別」への活用も

――容易ではない研究だと感じましたが、無事に問題を解決されたら、すごく大きな成果となりそうですね。一方、別の研究にも取り組まれていると伺っていますが、そちらの研究についても教えてください。

最もメインで取り組んでいるのは、ここまでお話しした研究ですが、それ以外にも、２つほど大きなテーマがあるので、それらについても簡単にお話しします。いずれも統計物理学の話です。

一つ目は、タンパク質が拡散していく際の拡散係数（＝拡散のしやすさを表す比例係数）に関する普遍的な法則を発見したという研究です。タンパク質は、ひも状の形をしていて、それが水溶液中をゆらゆらと揺らぎ、形を変えながら拡散します。液体中を粒子が拡散する場合、その拡散係数は粒子の半径に反比例しますが、タンパク質のように、球形の粒子ではなく、かつ、形を変えながら拡散する場合はどうなのか。その瞬間ごとに拡散性は変化するのではないか。また、そうだとすると、瞬間ごとの拡散係数はどう計算できるのか。それらの点を、今回の研究によって初めて明らかにすることができました。結果だけ言えば、タンパク質をある球形で特徴づける慣性半径Rg（タンパク質を構成する各分子の、全体の重心からの距離の二乗の平均）に、タンパク質を取り巻く水の層の厚さに相当するR0を加えたRg+R0に反比例する形で、瞬間ごとの拡散係数が決まっていることがわかりました。

――こちらはイメージしやすい内容でした。この場合、統計物理学はどう関係しているのですか。

拡散は、無数の分子のランダムな運動ですが、それを統計的に扱って拡散係数というマクロな量を導きます。それがまさに統計物理学の考え方そのものと言えます。その他にもこの研究の様々なところに統計物理学の考え方が活かされています。

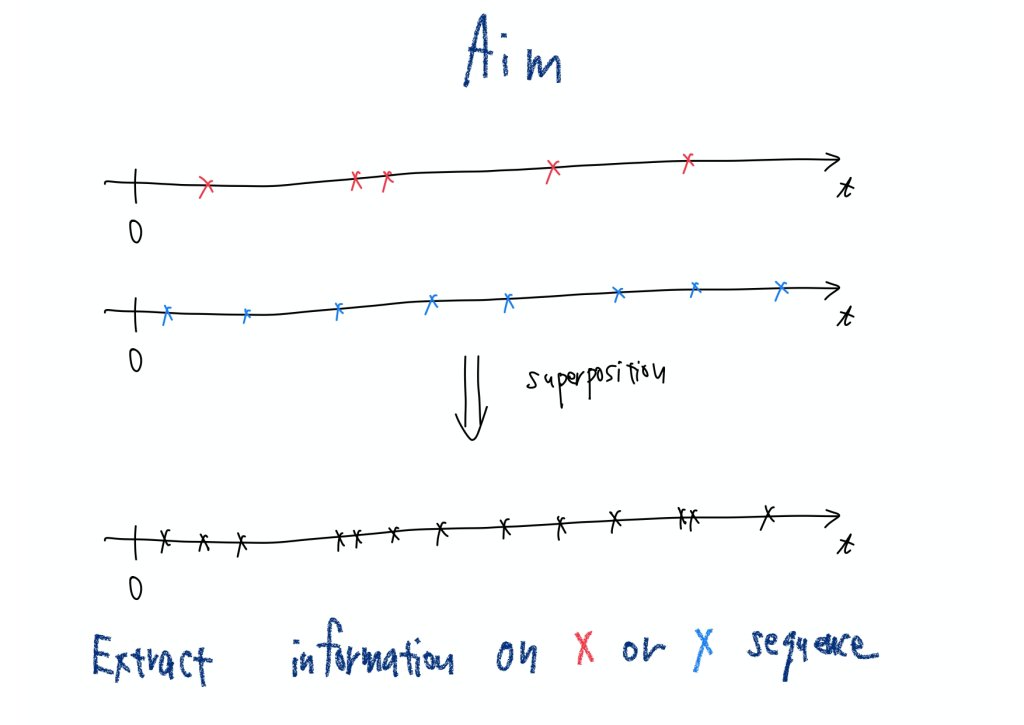
ではもう一つの研究にいきますが、こちらは地震に関連するものです。日本各地で本震がランダムに起こり、その各々に伴って余震が複数回発生するという具合に地震は日々起きていますが、時間軸上で考えると、軸の上に多数の点が打たれるような感じで発生していると言えるでしょう。このように、時間軸上の瞬間瞬間に突然イベントが起きるような過程をポイントプロセス（点過程）と呼びますが、この研究では、ポイントプロセスである地震データから余震だけを選び出す方法を確立するための研究を行っています。詳しい内容はここでは触れませんが、地震の本震は、独立してランダムに起こる一方で、余震は、本震に誘発されて、つまり本震と関連して発生します。このように、ランダムに起こる事象なのか、相関があって起こる事象なのかを解析するのは、まさに統計物理学の方法が用いられる典型的な問題です。例えばネットショッピングのサイトに書き込まれるレビューが、本物のレビューなのか”サクラ”レビューなのかを見分けるような方法も、同じようなアプローチで考えることができます。

――統計物理学は、経済や社会の問題などにも応用できるとおっしゃっていましたがまさにそのことを実感できる研究ですね。

未開の領域を切り開く“創域”の精神

――統計物理学は、いろいろな対象へ応用できるということが想像できるお話でした。その点で秋元先生の研究は“創域”と関連が強いのではないかと感じましたが、先生の“創域”についてのお考えを聞かせてください。

私は、“創域”とは「領域を創ること」、つまり未解決な分野を開拓していくというイメージを持っています。その意味で、自分にとっては非平衡・非定常の世界が“創域”の現場のように感じています。新しい領域を創っているとまでは言えませんが、統計物理学というすでにある程度確立された分野の中の未開領域を切り開いている感覚はあり、そこに自分は“創域”という意識を重ねています。また、先に少し触れましたが、数学理論を用いて物理現象を解明することで、数学と物理学を互いに発展させたいという気持ちも強く、その点も自分にとっては“創域”だと感じています。

東京理科大学には、4つの学部に「物理」が付く学科があります。理学部第一部と理学部第二部の物理学科、先進工学部の物理工学科、そして我々、創域理工学部の先端物理学科です。それぞれに特色があり、様々な形で物理学を学べるというのは本学の強みの一つですが、その中で、先端物理学科は、他分野との融合を意識した、分野横断的な物理学が学べることが特長と言えると思います。創域理工学部は、教員同士も異分野融合ということを意識していますし、そういうことが非常にやりやすい環境が整っています。そして、分野横断に留まらず、できれば新しい領域を創り出すところまで行こう、というのがこの学部のコンセプトなのだろうと私は考えています。

――秋元先生は、公開されている動画で、学生に対して研究室の選び方についてお話しされていたり、ウェブサイトでも、一緒に研究に取り組んだ学生の名前を前面に出されていたりと、学生の教育にとても力を入れられている印象を受けました。そのような秋元先生の教育への思い、そしてこれから創域理工学部を目指す高校生や、研究者を目指す若い世代にメッセージをお願いします。

そうですね、私は、研究活動を通じて学生を教育する「研究教育」には、意識的に力を入れています。研究を通じて人を成長させる、人材を育てるということは大学の一番の使命だと感じるからです。特にAIの発展が目覚ましい現在、知識を教えるだけだったら、今後大学は不要になっていくようにも思います。その一方、研究活動を通した教育は、大学以外ではなかなか難しいですし、それこそが大学が存在する意義なのだろうと感じています。

高校生の皆さんには、大学は、教育機関であると同時に研究機関であるという点を特に意識してほしいと思います。そこが高校とは全く違うところです。研究することを楽しみに大学に来てもらえたら嬉しいですね。研究は簡単ではありませんし、失敗やうまくいかないことにもきっと度々直面します。でも、仮に思ったような成果が出なくても、研究を論文にして世の中に出すことが重要であり、そこまでは確実にサポートする指導を、私は学生に対して行ってきました。論文を書くことはいろんな意味で将来につながります。真剣に研究をしたい人にはよい環境を提供できる自信はあるので、興味ある人は、ぜひ機会を見つけて野田キャンパスに訪ねてきてもらえたらと思います。