解析学 (偏微分方程式、非線形解析)

斬新なアイデアと研究室メンバーとのコミュニケーションで微分方程式を研究し、未来を解明する
自然現象も社会現象も解明する新たな微分方程式を求めて
自然界の多くの現象は、微分方程式で記述できます。たとえば、熱や波の伝搬、分子が流体中に拡散する様子、さらには震災復興のモデルやウイルスによる感染症拡大の様子なども。世の中のあらゆるものは時間の経過に伴って変化していきます。微分方程式は、時間の経過に伴うある量の変化を記述していますので、時間が十分経過したときの解の様子を調べることにより、未来の状況を解明できることになります。本研究室では、あらゆる自然現象の理解や予測に当てはめられる、新たな理論の開発を求めて、日々微分方程式の研究をしています。

膨大な計算と厳密な論証に向き合い答えという真犯人を追いかける
非線形の偏微分方程式の解の存在と一意性、解の漸近挙動についての研究を行っています。主な研究対象として、数理生物学に現れる走化性方程式系があげられます。多くの昆虫や動物は鋭い嗅覚をもっており、それに関わる化学誘引物質は、個体群に方向性のある運動をもたらします。そのような性質を「走化性」といいます。例えば細胞は、一度バクテリアに感染すると、バクテリアのいる方向に移動して攻撃を始めます。そうすると血中の白血球は濃度勾配を登り、バクテリアによる炎症が生じているところへ向かいます。このような細胞の動きを表すのが、走化性方程式です。
本研究室では、数学的観点から、そのような方程式の解の存在や性質を予想し、予想が正しいかどうかを研究しています。時には研究室の学生や海外の研究者と連携して膨大な計算と厳密な論証を行い、真相を解明していきます。これは、サスペンス映画や推理小説で犯人を絞り込んでいく作業に似ています。雲をつかむような状況に光を当て、存在するはずの真犯人に近づいていく。この研究分野にはそんな喜びがあります。
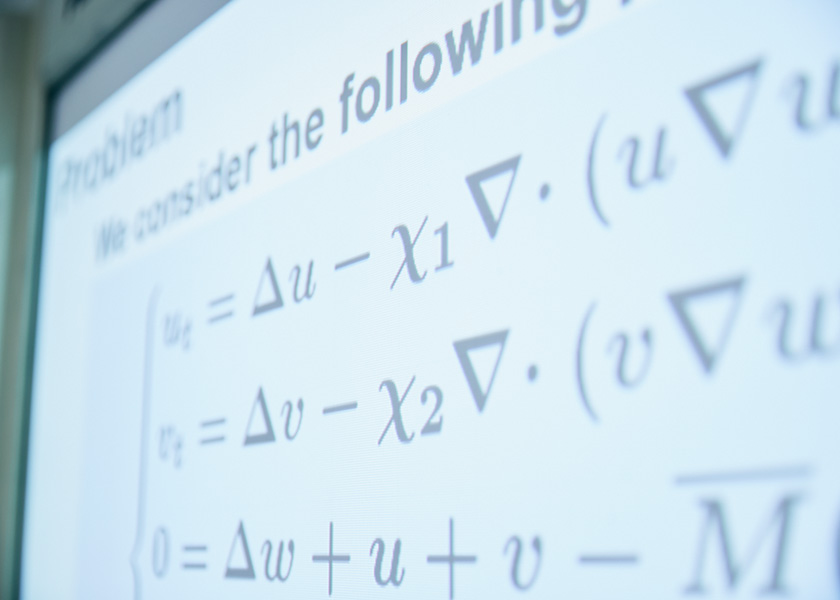
現在研究中の微分方程式 
研究のベースとなる数学研究室象徴の数学書 
先ずは直接手に持ってみることをモットーに研究に取り組んでいる
「分かる」より「分からない」経験こそ数学に、社会に活きる力が身についていく
数学の研究というと、黙々と数式と向き合い、一人でひたすら解いているイメージをされる方が多いかと思いますが、私の研究室では「人にわかりやすく、面白く伝える」をモットーにプレゼンテーションやグループワークを盛んに行なっています。
大学の数学では難解な理論が多いので、高校までの数学とは違って一人で解決できないことが増えます。そういったときに、友達や先輩とディスカッションするためには、自分のアイデアや問題の本質を理解していなければなりません。そして、楽しく議論することで新たな視点やアイデアが生まれて研究が一歩先へと進むことができます。だからこそコミュニケーションとユーモアが、数学には大切だと私は考えています。
また、私の研究室では、コンピュータによるシミュレーション等には頼らず、計算はすべて自分たちの手計算で行います。計算を進める過程で新しいアイデアを発見することが多いので、自分でコツコツと進めることが欠かせません。
そういった意味では、私の研究室では、「分かる」より「分からない」という経験をたくさんして、AIやコンピュータには備えつけられない能力が身につくのかもしれません。



