人間はなぜ音楽を聴くのか。音楽の数学的構造からその本質に迫る―情報計算科学科　大村英史講師に聞く―  

音楽とは、音が時間的に並んだ集合体であり、それだけで何か具体的な情報を表現することはできません。しかし私たちは、そのような音の集合を聞くことで楽しいと感じたり、感情を揺さぶられたりします。いったいそれはなぜなのか。大村英史講師は、音楽の持つその特性についてよりよく理解すべく、研究を続けています。音楽が数学的に構造化された情報であるということに着目し、その構造を紐解き、音楽の根本に立ち返ることで、その本質に迫ろうとします。私たちはどのような音の集合を音楽と感じるのか。時計の音や森の音とはどう違うのか、または違わないのか。それはなぜか。大村講師に聞きました。

大村英史（おおむら ひでふみ） 2002年 東京農工大学工学部機械システム工学科卒業。2009年 東京工業大学大学院博士課程修了。博士（工学）。科学技術振興機構 ERATO 岡ノ谷情動情報プロジェクト研究員、国立精神・神経医療研究センター 精神保健研究所 成人精神保健研究部 流動研究員などを経て、2015年より東京理科大学理工学部情報科学科 助教。同講師を経て、2023年、学部改称により現職。

音楽の背景にある数学的構造

――大村先生のご研究の概要を教えてください。

一言で言えば、「人間にとって音楽とは何か」を明らかにしたいという思いを起点として、音楽に関する様々な研究を行っています。音楽は、物理的には、音が時間軸上に並んでいるだけのものであり、何も具体的な情報なりを表現できるわけではありません。たとえばベートーヴェンの「運命」でも、タイトルがなければ、ただ曲だけを聴いて「これは『運命』だ」と感じる人は多くはないでしょう。つまり音楽は抽象的なものです。そのような抽象的な音楽を聴いて、私たちはなぜ、楽しいと感じたり、悲しい気持ちになったりするのでしょうか。それをよりよく理解するために、音楽が持つ数学的な構造に立ち返るといったことをしています。

――音楽が持つ数学的な構造とは、どのようなものなのでしょうか。

音楽はかつて、「耳で聞く数や量」と言われ、数学と同等な学問として扱われていた時代もありました。それくらい音楽と数学は密接にかかわっています。普段慣れ親しんでいる西洋音楽のようなものから離れ、音楽を音の連なりとして見つめ直すと、その意味が見えてきます。その際特に重要になるのが、音の連なりの中にある２つの要素です。一つは、音程。そしてもう一つが、音が出されるタイミングです。

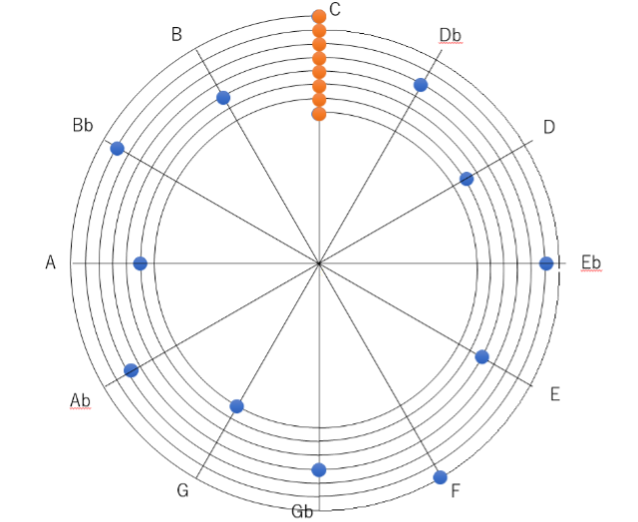
まずは音程について。音程とは、音と音の間の距離、つまり、２つの音の高さがどれだけ違うか、ということです。そもそも音の高さとは、空気が振動する速さ、すなわち周波数によって決まりますが、人間は、2つの音の周波数が2：3といった簡単な整数比で表される関係にある時、2つの音の響きを心地よいと感じることが古くから知られています。そういう2つの音の距離は「完全協和音程」と呼ばれます。完全協和音程には、周波数比で2：3、1：2または3：4の３種類があり、私たちはそれらの関係にある2音を、「近い関係の音」だと感じます。特に、ある音からその2倍の周波数（1：2の関係）を持つ音までを「１オクターブ」と呼びます。一方、ある音から順に、周波数がその3/2倍（2：3の関係）となる音を並べていくと、12個の音が表れます（ドから始めると、13音目で再びほぼドの音に戻る。下図参照）。その12音によって、私たちが普段用いる12音階（＝12音を並べたもの）ができています。そしてその12音の中で、明るい音楽が作られやすい7音の組み合わせが長音階（＝メジャースケール）、悲しげな音楽が作られやすい7音の組み合わせが短音階（＝マイナースケール）、といったあたりを基本として、各地域の文化的背景とも関連して様々な音階が作られてきました。

次に、音のタイミングについて。たとえば、時計の秒針のように1秒おきにカチッカチッと鳴る音があるとします。そこに0.25秒ごとに鳴る音を重ねると、つまり、周期の比が4：１となる２つの音を重ねると、４回に１回は両者が同時に鳴って強く聞こえ、いわゆる4拍子となります。そのように、音程と同様に、周期が簡単な整数比となる音を組み合わせて鳴らすと、いろんなリズムを作ることができます。

以上を基本として、たとえば音程が周波数比1：2や2：3となるいくつかの音を、周期も1：2や2：3といったリズムでランダムに鳴らすだけで、音楽と感じられるような音を作ることができます。

期待を裏切られることで心が動かされる

――音楽が持つ数学的な構造というのがよく想像できました。音楽をこのように捉えると、それがなぜ人間を感動させられるのかという点も考えやすくなりそうですね。

はい。まさにそのような観点から、なぜ音楽が人間を感動させられるのかが考えられてきた中で、20世紀の音楽学者レナード・メイヤーやユージン・ナームアは次のように言いました。「音楽は、次にどんな音が鳴るのかを聴取者に期待させ、その期待を裏切ることで人間の情動を引き出す」と。例えば、連続的にドの音が鳴る中で、たまにソが鳴ると、聴取者はそこに引っ掛かりを感じて反応する、といった具合です。

これは音だけに限ったことではなく、光や振動などに対しても、人間の脳は、期待とは異なる刺激によって特異な反応を示すことが生理学的に明らかになっています。音楽家は古くからそのことを直感的に理解していたのでしょう。例えば18世紀に活躍した音楽家ハイドンの傑作『驚愕』は、タンタンタンタンという音が続く中で、突然バンと大きな音を出すことで印象的な曲となっています。

――音が期待を裏切る、ということも数学的に考えることができるのでしょうか。

この点を考えるにあたっては、「エントロピー」の概念が有効です。エントロピーは複雑さや乱雑さ、不確実さの指標として、熱力学など、物理学の分野で使われてきた概念です。例として、コーヒーにミルクを入れる場合を考えると、ミルクを入れる前、両者が別々に存在する状態はエントロピーが低いけれど、ミルクを入れて、両者が複雑に混ざり合った状態はエントロピーが高い。これを音の連なりに当てはめて考えると、例えば、時計の秒針の音のように、ずっと同じリズムを繰り返すものはエントロピーが低く、そこに時々、他の音が入る、つまり期待を裏切るような音が入るとエントロピーが高くなる。そして、音程やリズムがより複雑になるほどに、エントロピーはさらに高くなります。

ダニエル・バーラインという学者は、人間と音楽の関係を、エントロピーによって論じました。すなわち、時計の秒針のように、ランダム性が非常に少なく、エントロピーが低い音の連なりは、聞いているだけで眠れなくなる人がいるぐらい人間にとって不快になりうる。一方、時計の秒針の音の裏拍（＝秒針の音と音の間）にポコッと何かが鳴るだけでも、面白く感じられる音になる。加えてさらに、ピッチ（＝音の高さ）の違う音が混ざったりすると複雑さは増し、面白みも増す。つまりエントロピーが高くなるにつれて、音楽は人間の情動をより強く引き出すものになる、というわけです。しかし、そのままどんどんエントロピーが高くなると、つまり音がさらに複雑さを増していくと、いずれリズムなどもよくわからなくなり、理解不能でうるさく感じられるようになる。すると音楽は心地よさを失い、再び不快なものになる、ということをバーラインは言いました。

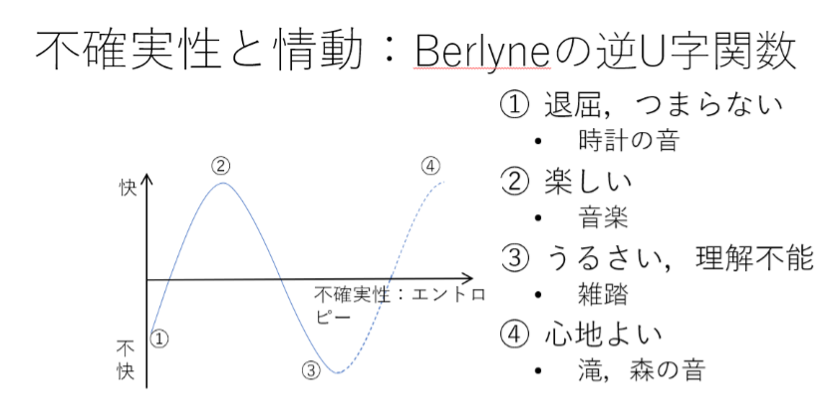
その説に対して私は、さらに先があるのではないかと考えています。つまり、バーラインの言う、音楽が不快になる段階を越えてさらにエントロピーが高くなると、今度は心地よくなるのではないか。例えば滝の音のように、高さもはっきりわからないような音をホワイトノイズと言いますが、それを心地よく感じる人は多い。波の音や森の音もそうです。森の中で鳥がいつ鳴くかはわからないけれど、突然鳴いても驚く人は少ないでしょう。つまり、ランダムであることがあたり前という状態までいくと、気持ちよくなるのではないか。それが私の仮説です。

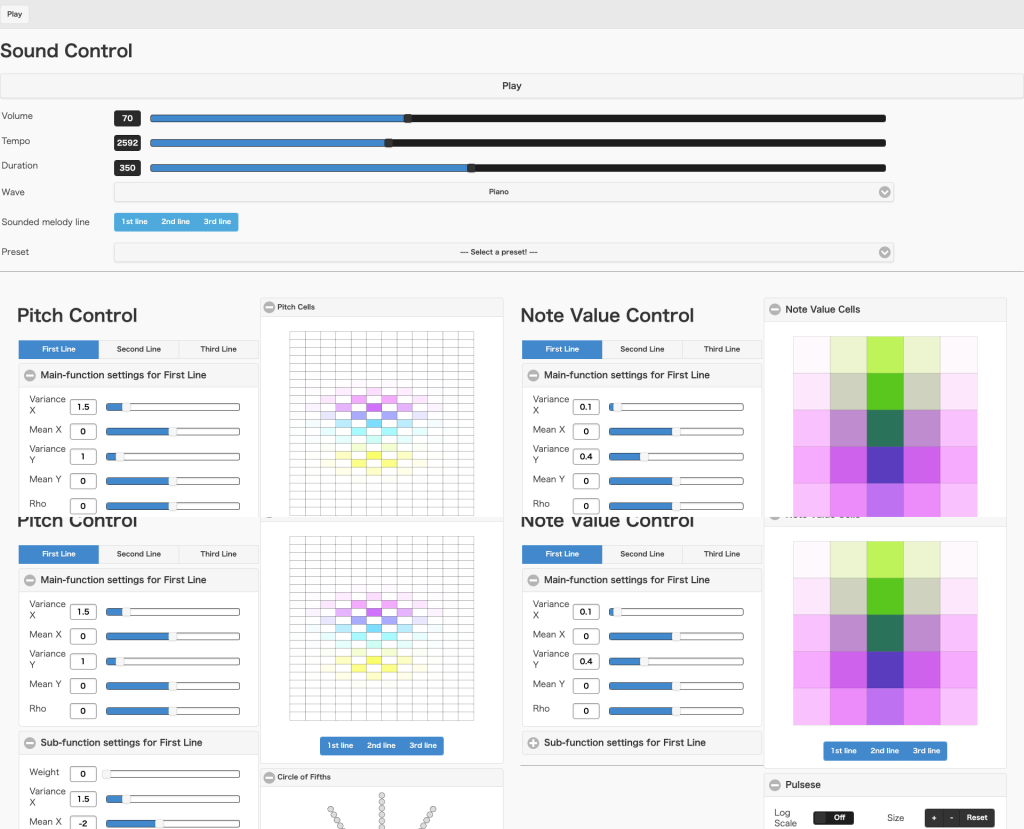
そうしたことを実際に確かめるために、私は一つのアプリケーションを作りました。様々なパラメータによって音のピッチとリズムを自由に設定し、エントロピーの低い音から高い音までを自由に作ることができるというものです。今後、これを用いて、音楽が人間の情動を喚起するメカニズムをさらに理解できるような何かを生み出していけたらと考えています。ちなみにこのアプリケーションは公開しています。興味のある方はぜひ実際に試してみてください。

https://ohmura.sakura.ne.jp/sc/music2/

音楽は音以外の要素もとても重要

――なるほど、音楽の数学的構造に着目して、その最も基本的な部分に立ち返ると、音楽がどのように人の心を動かすのかが見えてくるのですね。

ただ一方、音だけを分析しても音楽が人間に訴えかける力について完全には理解できません。私たちは音楽を聴くとき、音以外の要素からも大きな影響を受けているからです。例えばかつて、あるカリスマ的な作曲家の曲が実は別人によって作られていたことが発覚して、大騒ぎになったことがありました。するとその後、それまで素晴らしい音楽だと賞賛されていた曲も、作者が違ったということで評価が一変し、見向きされなくなりました。これはすなわち、私たちが、ただ音として音楽を聴いているわけではなく、作り手が誰かといった背景のストーリーを含めて音楽に感情を動かされていることを示しています。

また、ジョシュア・ベルという世界的なバイオリニストが、駅構内で路上ミュージシャン然として演奏してみると、ほとんど誰も耳を傾けなかったという実験があったり、ジョン・ケージという現代音楽の作曲家は、演奏者が何も音を出さない「4分33秒」という曲を発表し、その場の聴取者を含めた環境全体で自然に生じる微かな音のすべてが音楽となる状況を作り、音楽とは何かということを問いました。

これらの例から、音楽には、楽譜で表現される音以外の様々な要素が関係していることがわかります。そのことを、クリストファー・スモールという音楽学者は、「Musicking（ミュージッキング）」という言葉で表現しました。「音楽とは、行為であって物ではない。音楽は、関係するあらゆる行為によって構成されているのであり、それらすべてをミュージッキングと呼ぼう」と。私はそのような音楽の捉え方にとても興味を持っています。そうした点もいずれ、エントロピーの概念やその他数学的な方法によって分析することができたらと考えています。

“創域”は簡単ではないということを意識する

――音楽は、数学で表現できる論理的な構造を持つと同時に、簡単には定義できない複雑さを持ち合わせていることがわかりました。では、そのような音楽を研究される大村講師にとって“創域”とは何かについて、教えてください。

私は、現在は音楽に関する研究を中心に行っていますが、これまでかなりいろいろな分野に携わってきました。学部では機械を学び、大学院では人工知能を専攻しました。その後、一度就職してまたすぐに大学に戻り博士課程に進んだのですが、博士号を取った後は、科学技術振興機構（JST）のプロジェクトの研究員として情動の研究に携わり、その中で、音楽に関する研究に取り組むようになりました。しかしその後も、医療系の研究機関に所属したり、メディアアートの分野にも携わるなど、工学、理学のみならず、芸術や医学を含め、多様な分野の方たちとともに研究に取り組んできました。その全体を通底しているテーマは、人間とは何かを理解したい、ということであり、音楽はそうした中で主要な軸となってきました。

さて、そのような分野横断的な研究経験を通じて思うのは、分野を越えることは決して簡単ではない、ということです。工学と理学でも、話が通じないことは少なくないし、ましてや芸術、医学となってくると、全く世界が異なります。それゆえ、その間を隔てる壁を乗り越えて異分野の人と一緒にやっていくことは簡単ではないというのが私自身の実感です。それでも私が、異分野の方との研究を積極的に続けてきたのは、やはり刺激的だし面白いと感じるからです。しかし、壁を乗り越えることは簡単ではないと認識しておくことは重要だと感じます。

いまや分野を越えた“創域”的な研究をすることは確かに重要になっています。特に創域理工学部の中にいると、分野横断を意識する機会は多いはずです。だからこそあえて、それが簡単ではないということを強調しておきたいですし、そのことを意識した上で、“創域”に臨んでもらえたらと思っています。

――まさに“創域”的な研究を重ねてこられた大村講師の言葉ゆえに、響くものがあります。では最後に、高校生や研究に興味のある若い世代へのメッセージをお願いします。

“創域”的なものが求められる時代だからこそ、「自分はこの分野の専門家だ」と言える専門性をしっかりと持つことの重要性をぜひ意識してほしいです。加えて、自分のやりたいことを自分で見つける、ということもとても大切です。私は研究室の学生にいつも、自分の研究テーマは自分で考えて見つけてください、と伝えています。というのも、自分でテーマを設定する力、つまり、企画する力というのは、社会に出た時におそらく一番重要だからです。そして企画を実行したあとに、やったことをプレゼンテーションする力も重要です。

自分のやりたいことを見つけられるかどうかは、自分の意識にかかっています。ぜひいろんなことに興味を持って、これだという何かを見つけ、大学で深めていってもらえたらと思います。