役に立つからではなく、ただ面白いから研究する―数理科学科　側島基宏准教授に聞く―   

数学が面白いのは、自分の興味のままに研究でき、特許も権利も何も発生しないから――。そう話す数理科学科の側島基宏准教授は、掘り下げたいと思ったテーマにとことん向き合い続けてきました。現在は、偏微分方程式に出てくる「微分作用素」について研究しています。現実の現象を記述するのに必須である偏微分方程式の一部分を成す微分作用素の本質に迫りつつ、あくまでも研究は「自分が楽しいと思うからやっている」という立場。“創域”に関しても一貫してその立場を堅持する准教授の言葉からは、研究することの根幹にある楽しさや、そして、創域の新たな一面が見えてきます。

側島 基宏（そばじま　もとひろ） 東京理科大学で博士（数学）課程を修了後、イタリアのUniversita del Salento Dipartimento di Matematica e Fisica “Ennio de Giorgi”にてポスドク研究員を務める。帰国後、東京理科大学理学部第一部数学科 ポスドク研究員、同大理工学部数学科 嘱託助教、同講師などを経て、2024年4月より現職。

「微分作用素」とは何か

――先生のご研究の概要を教えてください。

私は、大きな枠組みとしては、数学の偏微分方程式について研究しています。偏微分方程式とは、微分方程式（＝ものの変化の仕方を記述する方程式）の中でも、変数が複数あるもののことで、その中に、「微分作用素」と呼ばれるものが出てきます。微分作用素とは、ざっくり言えば、「微分（＝変化率を求めること）せよ」という指示のようなものです。それがいろんな式にいろんな形で出てくるのですが、それらの中にある普遍性、または共通する性質を理解したいというのが、現在の私の研究の核となる部分だと言えます。

ここで一つ具体的な例をあげると、代表的な偏微分方程式に、「熱方程式」と呼ばれるものがあります。時間とともに熱がどう広がっていくか、ということを考えるときに使われる式なのでそう呼ばれます。たとえば、長い針金があり、その一点に熱を加えるという場合を考えてみましょう。この時、時間の経過とともに針金の温度がどう変化するかを知るために使うのが次の式です。

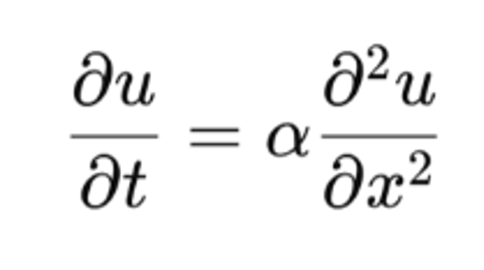
ここで、u(x,t)は、位置x, 時間tにおける温度、αは熱伝導率。この式が1次元の熱方程式です。この時、左辺はuを時間（t）で微分していて、右辺はuを空間（x）で2階微分していますが、それを表す部分（＝演算子）、下記が微分作用素にあたります。

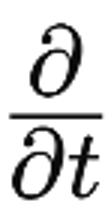
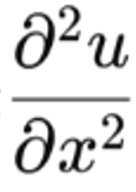
一方、この方程式の解の1つをxu平面上に書くと、次のようなグラフになります。

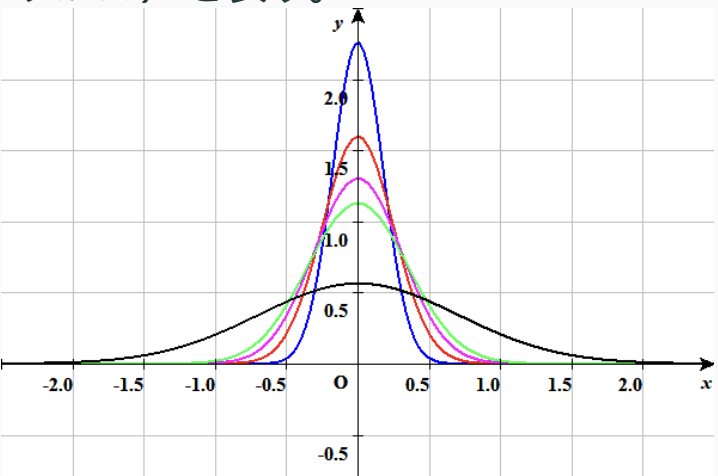
  つまり、ｘ軸と平行に針金が置かれ、原点にあたる位置に熱を加えたとすると、まず、原点の温度が上がり、その後、熱が徐々に針金全体に広がっていくというイメージです（青→赤→紫→緑→黒とグラフが変化する）。これは感覚的にも理解しやすいと思います。

微分作用素「ラプラシアン」の本質に迫りたい

さて、ここからが私が取り組んでいる研究の話になりますが、今度は、上のように一点に熱を加えつつ、同時に、その一点に冷却装置のようなものを置いて、針金を冷やしていく場合を考えてみましょう。また同様にして、2次元、3次元の場合、つまり、長い針金の代わりに広い平面と大きな球体の中心に冷却装置を置く場合も考えます。そして各々の状態を偏微分方程式で表し、それらを解き、中心から少し離れた場所で温度がどう変わるかを各ケースで調べます。

するとどうなるかと言えば、まず球体の場合、つまり3次元の場合は、冷却装置があっても系全体の熱の広がり方は、それがない場合とほとんど変わらないことがわかります。同様に、3次元以上のすべての次元の場合で、熱の広がり方は冷却装置があってもなくてもほとんど変わらないことが計算するとわかります。しかし一方、針金と平面の場合、つまり1次元と2次元の場合は、わずかな冷却装置が１つあるだけで、系全体の熱の広がり方に大きな変化が表れるのです。

何が言いたいのかと言えば、このように、熱方程式においては、1次元と2次元の場合だけ方程式の振る舞いが異なります。私は、その原因は、この方程式に表れる「ラプラシアン」と呼ばれる微分作用素の持っている性質にあると考えています（ラプラシアンとは、複数の変数に対する2階の偏微分を足し合わせる演算子のこと。上の１次元の熱方程式で言えば、

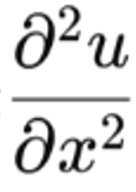
の部分にあたる。3次元の場合、

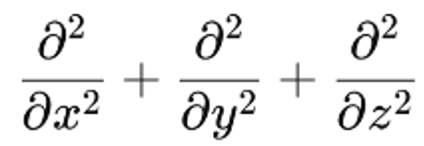
となる。）

もしそうだとすれば、ラプラシアンが登場する他の様々な方程式、すなわち、ポアソン方程式（重力場などを考える場合に使われる）や波動方程式（音や光の振動などを考えるときに使われる）などにも、同じような現象（＝1次元、2次元だけ振る舞いが異なる）が見られるはずだと考えていて、それらに共通する「何か」を探るというのが、現在の私の中心的なテーマとなっています。

――なるほど……。ひと言でいえば、ラプラシアンの本質的な性質を解き明かそうという研究、ということになるのでしょうか。

はい、そういってもよいかもしれません。私はそういう気持ちで取り組んでいます。一方、念のため補足すると、上で熱方程式の話をしましたが、私の研究では、物理現象としての熱について考えるわけではありません。熱方程式の数学的な側面が興味の対象であり、その意味をわかりやすく説明するために針金を熱するというたとえを用いたと考えてください。

――微分作用素の性質を深く掘り下げる、というところに興味が向かったのはどういう経緯があるのでしょうか。

学生のころ、指導教員に「この論文を読んで」と言われるままに論文を読んでいるうちに、気づいたらいまのような研究をするようになった、というのが率直なところです（笑）。ただ、研究を続けるうちにこの分野への興味が深まり、その後、自分にとっては大きな転機がありました。2019年に、先の熱方程式から派生する重大な問題の一つを、自分で考えた方法で解くことができたことです。それは誰も解けずに残っていた問題で、私はその背景なども知らずに、偶然解いてしまったんです。その時は、その問題が解けたことの意味をよくわかっていなかったのですが、その後、研究を続けていく中で、その性質は波動方程式にも受け継がれているということがわかってきました。そして現在の研究へとつながっていったという具合です。言葉ではどうしても抽象的になり、なかなかすっきりとは説明ができないのですが……。

――細部はとても複雑そうですが、現在の研究の背景に、ご自身による大きなブレイクスルーがあったということがわかりました。

「ダブルラボ」から得られた新たな視点と学生のモチベーション

――数学を研究する方に対して愚問かとは思いつつ、あえて伺いますが、この研究が進んでいくと、何かに応用できるとかそういう可能性があるのでしょうか。またこの研究を通じて他の分野の研究者とつながって創域的なことが進んでいくとか、そういうことはありそうでしょうか。

いや、そういうことは全く考えていません。あくまでも自分の数学的な興味に起因した研究であり、ここから直接的に他の分野の研究者とつながって何か社会に有用な研究に発展する、という可能性はほぼないと思っています。

ただ一方、“創域”の環境にいる中で思わぬ展開もありました。数理科学科では、創域的な取り組みの一つとして現在、4年生が他学科の研究室の下で「ダブルラボ」というプログラムを行っているのですが、そのプログラムで、うちの研究室の学生も、他の複数の研究室にお世話になったりしています。そうした中である学生が、情報計算科学科の研究室で研究させてもらうことになったのですが、その学生は、そこで量子情報について興味を持つようになり、プログラムが終わると、「作用素環」について学びたいと言って、大学院で私の研究室に入ることになりました。作用素環というのは、簡単に言えば、無次元の行列のようなものを考える数学の分野で、量子コンピュータにおいて重要な役割を果たしています。私はその専門家ではないので困ったのですが、とにかくその研究をしたいということで、私も一緒になっていろいろ調べたりするようになりました。そうしてやっているうちに、作用素環の理論を学ぶことが将来的に、いま私が取り組んでいる研究にもいい影響を与える可能性もあると感じるようになり、私自身、思わぬ形で新たな視点をもらうことになりました。それもまた、創域の一つの形なのかなと思っています。

――なるほど、学生が他の分野に通じることで、先生ご自身の研究が広がっていくことになったのですね。

そうですね。また、この学生以外にも、ダブルラボを通じて数学をやるモチベーションが上がったと言う学生が複数いて、それはうれしい発見でした。一方、私自身は、他の教員と何か創域的なことをしているかいうと、あまりしていません。スペシャリスト同士が一緒に何かをやろうとするといろんな意味でぶつかってうまくいかないという印象があるからなのですが、そうした中で、学生同士が分野を越えて交流することを通して、その結果、教員もまた、分野が広がったり、新たなつながりができたりするという可能性を感じ、それは創域の一つの側面として、いいなあと感じています。

特許も権利も何も発生しないという素晴らしさ

――側島先生にとって、数学を研究する面白さとはどのような点にありますか。

好き勝手できるところ、ですかね。ただ自分が好きだからやる、というだけ。自分の趣味を突き進んで、特許も権利も何も発生しない世界というのが私は素晴らしくいいなと思っています。例えばつい10日前に発表された論文の手法を使っても、お金が発生するということはないし、すごい結果を出したからといってお金がもらえるわけでもありません。ただ、名前が残る。あの定理はすごい、と言ってもらえる。それが数学の世界であり、私にとってはそれが数学を研究する大きな魅力だと感じています。いま取り組んでいる研究も、特にこれをやったから何になるというわけではありません。でも、「楽しいからいいじゃん」って思える。それは、自分にとって研究するうえで大切なことです。

――いまはどんな研究をする場合も、どう役に立つのかを問われることが多いと思います。その中で、側島先生のように、「役に立つかどうかは関係なく、ただ面白いから研究する」とおっしゃる方がいることは貴重だと感じます。

「役に立つかどうか」という、自分の興味とは別の要請があるのは研究するうえで辛くないのかなと自分は思ってしまいます。20年ほど前、ニュートリノの研究でノーベル物理学賞を受賞した小柴昌俊さんが「この研究は何の役に立つのですか？」と聞かれて、「そんなの何の役にも立ちませんよ」って言っていたのがとても印象に残っています。私は、小柴さんのように考える方の研究がもっと日本で大きくなってほしいなって思います。正直、“創域”って言われると、「イノベーションを起こしてお金を生み出せ」って言われている気もしてしまうのですが(笑)、自分のようなスタンスの研究者でも、気兼ねなく自由に研究ができるのもこの学部のよいところと言えるかもしれませんね。

――役に立つかどうかという視点から離れて、ただ面白いから研究するということの大切さを改めて感じます。最後に、研究者を目指す若い世代や高校生にメッセージをお願いします。

数学をやりたい人に向けたメッセージになるかもですが、問題を解くとき、大切なのは正しい答えを求めることではありません。答えは間違っていてもいい。ただ、自分がどう考えたのかをちゃんと説明できるようになる、ということを意識してほしいと思います。私は高校時代、できる学生では全くありませんでした。浪人もしていますし、その上、東京理科大は補欠合格でした。大学では教員に、「きみは数学に向いていない」と言われたこともあります。ただ、昔から数学に関しては、面白くてずっと問題を考えていました。この問題はどうやったら解けるんだろうと。考えていることが好きでした。結果としては、そうして考え続けていた時間が、いま活きています。考える時間こそが大事だと、いまつくづく感じます。
数学をとことん考え、数学で好き勝手に遊びたい、という人がもっと入ってくれたら私としてはうれしいです（笑）。